This section describes the Analytic material model.
Simple example
Suppose we have two materials: material A has a refractive index of na and material B has a refractive index of nb. These two materials can be combined to produce a composite material. The refractive index of this composite material is simply the weighted average a of the refractive index of the two base materials, as shown in the following formula.
$$index=n_a\alpha+n_b(1-\alpha)$$
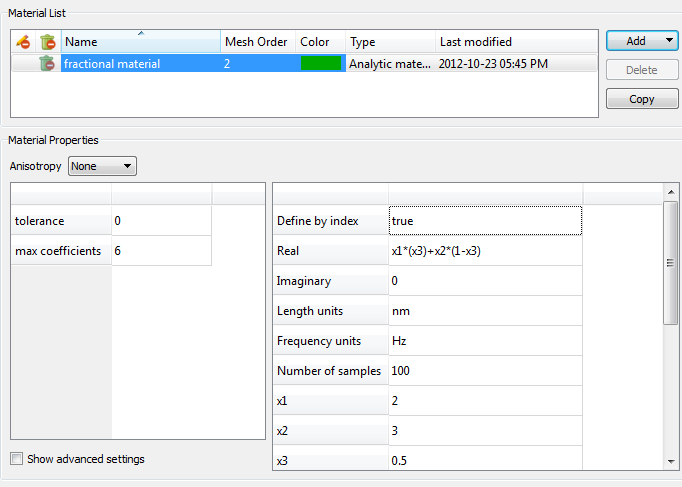
This type of material model can be implemented in the material database using the Analytic material model. This model makes it possible to define a material via an analytic function. In this case, our function has three variables: the index of materials A and B, and the fraction of material A in the mixture. The variables of the analytic model have fixed names, such as x1, x2, x3 and so on. Therefore, we must write the formula as:
$$index=x_1x_3+x_2(1-x_3)$$
where \( x_1=n_a, x_2=n_b, x_3=\alpha \)
FDTD example
It is important to understand that the analytic equation is not directly used in the simulation. It is necessary for FDTD to create a 'fit' for this material, in the same way that it must fit the Sampled data materials. In this example, the fit is perfect because the material is a simple lossless, non-dispersive model. For more complex materials, the quality of the fit may be lower.
It's always a good idea to use the Material explorer to check the quality of the fit, just like you should check the fits of Sampled data materials.
MODE example
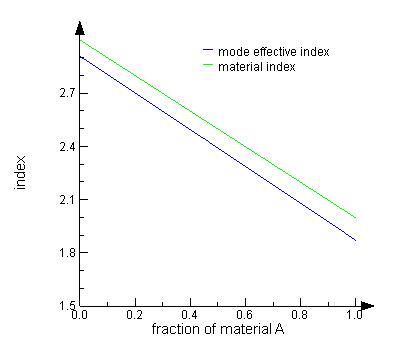
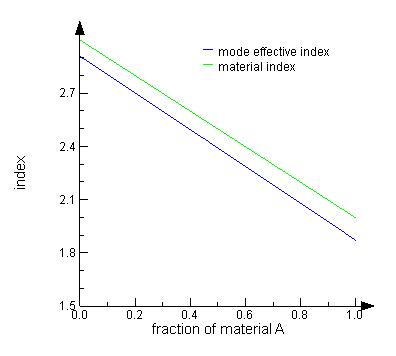
The simulation files usr_analytic_material1.fsp and usr_analytic_material1.lms contain this material. Using MODE, open the lms file, then run usr_analytic_material1.lsf to calculate the effective index of the fundamental mode as a function of the weighted average a. The following figure shows the final result of the simulation. The blue line shows the effective index of the mode, while the green line shows the actual material index, as calculated via the above formula. As expected, the mode effective index is always less than the material index.
For dispersive materials where the index or permittivity are defined as complex equations, please see Importing arbitrary dispersive models
|
Note: The predefined variables that can be used in the equations for "real" and "imaginary" are:
|